My Account
- Log In
  
  New to Edmund Optics^®? Register.
0
Cart

Ball Lens Calculator

View All Technical Tools

Ball Lens Material:n: -- D:d:

EFL (mm) : --
BFL (mm) : --
NA: --

$$ \text{EFL} = \frac{n \, D}{4 \left( n - 1 \right)} $$

$$ \text{BFL} = \text{EFL} - \frac{D}{2} $$

$$ \text{NA} = \frac{2 d \left( n - 1 \right) }{n \, D} $$

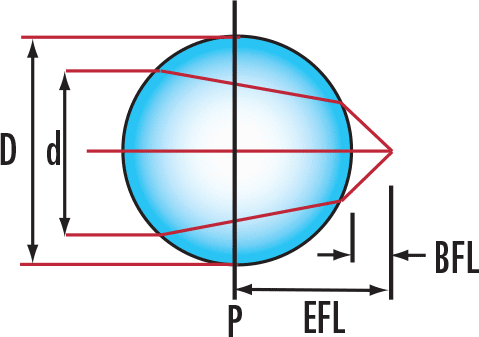
EFL	Effective Focal Length
BFL	Back Focal Length
NA	Numerical Aperture

n	Refractive Index
D	Diameter of the ball lens
d	Diameter of the input source

Notes:

Please use the American standard for number formatting rather than the European standard (i.e. for "two and a half," enter "2.5" rather than "2,5").

Description

Determine the effective focal length, the back focal length, and the effective numerical aperture of a ball lens based on its diameter, its refractive index, and the diameter of the collimated beam entering or exiting the ball lens. The effective numerical aperture of the application can only be calculated if the user knows the beam diameter. Knowing the numerical aperture is particularly useful when using ball lenses to couple light from a fiber to a laser or to another fiber.